Tutorial DEAP
Problema da fabricação de garrafas
TL;DR
Neste post eu quero mostrar a utilização de um framework para computação evolucionária chamado DEAP(Distributed Evolutionary Algorithms in Python). Como o nome já diz é uma lib de algoritmos evolucionários que podem ser rodados de forma distribuidas. Ah, e é em Python! =)
Descobri esse framework quando fui buscar uma solução(em Python) que me auxiliasse em alguns trabalhos da disciplina de Computação Evolucionária que estava fazendo no mestrado. Confesso que no inicio demorei para pegar o jeito, pois a biblioteca tem uma forma peculiar de definir os operadores e funções. Porém depois de compreendido, não quis outra vida! se torna natural pensar nas soluções. Just sit and code!
O que coloco abaixo é um Toy Problem sugerido pelo professor da disciplina. O notebook que eu fiz pode ser encontrado nesse link e tem praticamente o conteudo abaixo(que exportei para colocar aqui no blog)
DESCRIÇÂO DO PROBLEMA
Você gerencia uma fábrica de garrafas plásticas que tem apenas uma máquina extrusora. Esta máquina pode funcionar até 60 horas por semanda, isto é, 6 dias por semana com jornada de 10 horas por dia. A máquina é capaz de produzir dois tipos de garrafas plásticas: tipo “leite” e tipo “suco”. Toda a produção semanal de garrafas plásticas é armazenada temporariamente num depósito. No domingo toda a produção é despachada para os compradores e o depósito é esvaziado completamente.
A linha de produção leva 6 horas para produzir 100 garrafas tipo leite e 5 horas para produzir 100 garrafas tipo suco. Cada Carrafa tipo leite ocupa 10 unidades cúbicas de espaço no depósito, enquanto que a garrafa de tipo suco ocupa 20 unidades cúbicas. O depósito tem capacidade máxima de 15000 unidades cúbicas.
A contribuição no lucro final da empresa por garrafa tipo leite é de 5 unidades monetárias e por garrafa tipo suco é de 4,5. O departamento de vendas tem contratos de fornecimento capazes de absorver toda a produção possível de garrafas tipo suco, porém tem compradores somente para 800 garrafastipo leite por semana.
Você deve estabelecer qual é o plano de produção mais adequado para maximizar o lucro total da empresa, isto é, quantas garrafas tipo Leite e quantos tipoo Suco devem ser produzidas semanalmente.
Import dos pacotes
O DEAP fornece várias bibliotecas que facilitam o trabalho e deverão ser importadas:
- base:
- creator:
- tools:
- algorithms:
Outras blibliotecas auxiliares serão utilizadas nesse tutorial: - random: - numpy:
import random
import numpy
from deap import base
from deap import creator
from deap import tools
from deap import algorithms
# INIT
toolbox = base.Toolbox()
Natureza do problema
Como se trata de um problema de maximização criamos essa função conforme a especificação do DEAP
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
Individuos e população
Cada problema necessita uma forma particular de modelar o individuo, bem como a população deve ser gerada. Sendo assim os passos que devemos fazer no DEAP são: - Definir estrutura do individuo(list, set, etc) - Definir a função que irá gerar os alelos - Definir a função que irá gerar os individuos - Definir a função que irá gerar a popuulação
# Definindo a estrutura do indivíduo
IND_SIZE = 20 # Tamanho do individuo - 10 para cada gene
GENES = 2
creator.create("Individual", list, fitness=creator.FitnessMax)
# funcao para gerar o gene com alelos 0 ou 1 randomicamente uniforme
toolbox.register("attr_bool", random.randint, 0, 1)
# funcao para gerar o indivíduo (nome, forma de gerar, Estrutura, funcao geradora, tamanho)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n=IND_SIZE)
# funcao para gerar a populacao
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
Função de fitness
Essa função ao contrário das outras que são produzidas quase que parametricamente, deve ser impllementada manualmente. Nela é onde o individuo receberá o valor de fitness que corresponde à modelagem funcional do problem. Para o caso deste exemplo em questão temos:
# funcao de fitness
def evaluate(individual):
l = int("".join(str(i) for i in individual[:int(IND_SIZE/GENES)]), 2) # gene quantidade de garrafas de leite
s = int("".join(str(i) for i in individual[int(IND_SIZE/GENES):]), 2) # gene quantidade de garrafas de suco
g = (5 * l + 4.5 * s) / 9718.5 # funcao objetivo normalizada [0,1]
h1 = max(0, ((6 * l + 5 * s) / 100 - 60)) / 52.53 # funcao de restricao 1 normalizada [0,1]
h2 = max(0, (10 * l + 20 * s - 15000)) / 15690 # funcao de restricao 2 normalizada [0,1]
h3 = max(0, (l - 800)) / 223 # funcao de restricao 3 normalizada [0,1]
h4 = max(0, (s - 750)) / 273 # funcao de restricao 4 normalizada [0,1]
return g - 2*(h1+h2+h3+h4)/4, # fitness normalizado [0,1]
Operadores
Para o DEAP são considerados como operadores: - evaluate: operador para realizar o cálculo de fitness do indivíduo - mate: operador para realizar cross over de indivíduos - mutate: operador para realizar a mutação dos - select: operador para selecionar os melhores de uma geração para outra
Cada um desses operadores deve ser registrado. Seguindo a documentação do DEAP, damos um nome para o operador, seguido da função que ele irá realizar, seguido dos parametros dessa função
# registra funcao de fitness
toolbox.register("evaluate", evaluate)
# registra crossOver
toolbox.register("mate", tools.cxTwoPoint)
# registra mutacao com probabilidade default de mudar cada gene de 5%
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
# registra o metodo de selecao como torneio de tamanho 3
toolbox.register("select", tools.selTournament, tournsize=3)
Funções adicionais
Dependendo de cada caso, podemos desejar mostrar relatórios específicos. Para esse problema, criamos duas funçõs. Uma para imprimir os dados de um indivíduo e outra para plotar o gráfico das evoluções das gerações.
#Imprimir indivíduo
def print_ind(individual):
l = int("".join(str(i) for i in individual[:int(IND_SIZE / GENES)]), 2) # gene quantidade de garrafas de leite
s = int("".join(str(i) for i in individual[int(IND_SIZE / GENES):]), 2) # gene quantidade de garrafas de suco
g = 5*l + 4.5*s
print('Individuo:' + str(individual))
print('Quantidade de garrafas de leite: ' + str(l))
print('Quantidade de garrafas de suco: ' + str(s))
print('Lucro: ' + str(g))
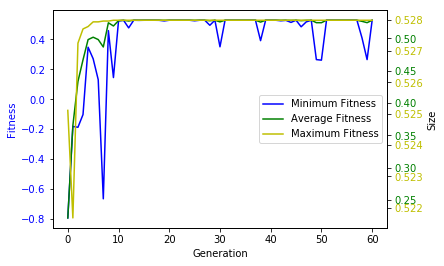
#Plotar Gráfico
def plot_log(logbook):
gen = logbook.select("gen")
min = logbook.select("min")
avg = logbook.select("avg")
max = logbook.select("max")
import matplotlib.pyplot as plt
fig, ax1 = plt.subplots()
line1 = ax1.plot(gen, min, "b-", label="Minimum Fitness")
ax1.set_xlabel("Generation")
ax1.set_ylabel("Fitness", color="b")
for tl in ax1.get_yticklabels():
tl.set_color("b")
ax2 = ax1.twinx()
line2 = ax2.plot(gen, avg, "g-", label="Average Fitness")
for tl in ax2.get_yticklabels():
tl.set_color("g")
ax3 = ax1.twinx()
line3 = ax3.plot(gen, max, "y-", label="Maximum Fitness")
ax3.set_ylabel("Size")
for tl in ax3.get_yticklabels():
tl.set_color("y")
lns = line1 + line2 + line3
labs = [l.get_label() for l in lns]
ax1.legend(lns, labs, loc="center right")
plt.show()
Algoritmo
Depois de definir toda a estrutura do nosso problema e o comportamento, faz-se necessário implementar o algoritmo que irá rodar. Essa implementação é composta dos parametros do Algoritmo Genético e a logica que manipula a população.
No exemplo abaixo utilizamos uma implementação já fornecida pelo DEAP: o eaSimple que é um algoritmos do livro “Evolutionary Computation 1 : Basic Algorithms and Operators”(cap.7). Neste exemplo também optei poro trazer uma implementação mais enxuta sem mostrar os stats monitorados no console, de modo apenas focarmos no processo como um todo do AG.
def main():
random.seed(94)
# cria populacao inicial
pop = toolbox.population(n=70)
# CXPB - probabilidade de crossover
# MUTPB - probabilidade de mutacao
# NGEN - numero de geracoes
CXPB, MUTPB, NGEN =0.8, 0.02, 60
#stats a serem guardados
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register("std", numpy.std)
stats.register("min", numpy.min)
stats.register("avg", numpy.mean)
stats.register("max", numpy.max)
#Roda o algoritmo
pop, logbook = algorithms.eaSimple(pop, toolbox, CXPB, MUTPB, NGEN, stats=stats)
#Seleciona o melhor individuo da populacao resultante
best_ind = tools.selSPEA2(pop, 1)
#Imprime as infromações do melhor individuo
print_ind(best_ind[0])
#Plota o Gráfico
plot_log(logbook)
if __name__ == "__main__":
main()
gen nevals std min avg max
0 70 0.279164 -0.794191 0.222211 0.5251
1 53 0.137051 -0.182224 0.365127 0.521669
2 57 0.104841 -0.18801 0.433291 0.527247
3 62 0.0855094 -0.102859 0.466715 0.5277
4 61 0.0348315 0.347647 0.498005 0.527777
5 58 0.0463223 0.270386 0.501738 0.527926
6 52 0.0528416 0.130146 0.498091 0.527926
7 50 0.169755 -0.666382 0.48663 0.527952
8 44 0.0118609 0.458677 0.524036 0.527952
9 58 0.0480039 0.144649 0.519095 0.527978
10 61 0.0011975 0.523538 0.527375 0.527978
11 58 0.000187768 0.527242 0.527867 0.527978
12 60 0.00671136 0.476925 0.52684 0.527978
13 58 1.28367e-05 0.527926 0.527958 0.527978
14 50 0.000147406 0.527242 0.527935 0.527978
15 62 1.45458e-05 0.527864 0.527974 0.527978
16 46 1.11022e-16 0.527978 0.527978 0.527978
17 53 1.11022e-16 0.527978 0.527978 0.527978
18 58 5.37505e-05 0.527525 0.527971 0.527978
19 52 0.000526875 0.523538 0.527914 0.527978
20 66 1.11022e-16 0.527978 0.527978 0.527978
21 58 1.11022e-16 0.527978 0.527978 0.527978
22 60 1.11022e-16 0.527978 0.527978 0.527978
23 61 1.11022e-16 0.527978 0.527978 0.527978
24 58 1.11022e-16 0.527978 0.527978 0.527978
25 64 0.000424759 0.524464 0.527917 0.527978
26 60 1.11022e-16 0.527978 0.527978 0.527978
27 58 1.11022e-16 0.527978 0.527978 0.527978
28 52 0.00452791 0.494315 0.527231 0.527978
29 60 1.11022e-16 0.527978 0.527978 0.527978
30 64 0.0210769 0.350363 0.52544 0.527978
31 56 1.11022e-16 0.527978 0.527978 0.527978
32 56 1.11022e-16 0.527978 0.527978 0.527978
33 57 1.11022e-16 0.527978 0.527978 0.527978
34 48 1.11022e-16 0.527978 0.527978 0.527978
35 56 1.11022e-16 0.527978 0.527978 0.527978
36 52 1.11022e-16 0.527978 0.527978 0.527978
37 58 1.11022e-16 0.527978 0.527978 0.527978
38 52 0.0177761 0.391521 0.525117 0.527978
39 62 1.11022e-16 0.527978 0.527978 0.527978
40 56 1.11022e-16 0.527978 0.527978 0.527978
41 52 1.11022e-16 0.527978 0.527978 0.527978
42 62 0.000416938 0.524464 0.527927 0.527978
43 54 0.000107501 0.527072 0.527965 0.527978
44 64 0.00171128 0.513557 0.527772 0.527978
45 52 1.11022e-16 0.527978 0.527978 0.527978
46 58 0.00519679 0.48418 0.527341 0.527978
47 54 0.00133758 0.516706 0.527817 0.527978
48 64 1.11022e-16 0.527978 0.527978 0.527978
49 56 0.0312358 0.264753 0.524217 0.527978
50 54 0.0316754 0.261049 0.524164 0.527978
51 52 1.11022e-16 0.527978 0.527978 0.527978
52 50 1.11022e-16 0.527978 0.527978 0.527978
53 54 1.11022e-16 0.527978 0.527978 0.527978
54 56 1.11022e-16 0.527978 0.527978 0.527978
55 66 1.11022e-16 0.527978 0.527978 0.527978
56 56 1.11022e-16 0.527978 0.527978 0.527978
57 54 1.11022e-16 0.527978 0.527978 0.527978
58 52 0.0140437 0.409631 0.526287 0.527978
59 45 0.0312358 0.264753 0.524217 0.527978
60 62 1.11022e-16 0.527978 0.527978 0.527978
Individuo:[1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0]
Quantidade de garrafas de leite: 672
Quantidade de garrafas de suco: 394
Lucro: 5133.0
Por hoje é isso. Espero que essa dica tenha ajudado a facilitar a sua vida.
Até mais!
